Alexander the Great (356 BC – 323 BC) is thought to be one of the best military generals of all time. He was twenty when he succeeded his father as the king of a Greek region called Macedon and within ten years, he had expanded his empire all the way till northwestern India. Here is a story from about two years after he became king.
Alexander was conquering the kingdom of Phrygia – now a part of Turkey – at this point. He came to know of a local legend that he thought could help him legitimize his rule in the eyes of the vanquished people. In the palace of a Phrygian city called Gordium was an ox-cart dedicated by an earlier king to the gods. The yoke of the cart had been tied with several knots all so tightly entangled that it was impossible to see where the rope started or ended. An oracle had famously declared that the person who undid the knot would rule all of Asia.
After trying for some time to untie the knot but making no headway, Alexander realized that the oracle’s prophecy did not specify how the knot should be loosened and so untying it need not be the only way. He pulled out his sword, and with a single stroke, cut the knot in half.
The general population accepted that the oracle’s prophecy had been fulfilled and, therefore, believed that Alexander was destined to be the ruler of not only their land but whole Asia. This was undoubtedly a huge public relations victory for Alexander.
Keep this story in mind. We’ll circle back to it at the end of this article.

Among the GRE students I have interacted with over time, I have realized that many do not do enough review and reflection for the concepts they have studied and the questions they have solved.
‘Not enough’ is both a quantitative problem – meaning that the number of concepts and questions that they revise is lesser than it could be – and a qualitative problem – meaning that for the things that they do revise, their revision is not as rich and useful as it could be.
How does one decide which questions to revise?
Many students use just one criterion: accuracy; they revise a question only if they got it wrong. So, unreviewed go many questions where their correct answer was only a lucky guess or questions where their correct answer cost them ten minutes, a time that they cannot afford to spend in the actual test. Even the revision and reattempt of previously incorrectly answered questions lasts only till the student remains underconfident about solving such questions.
It is a common misconception that once a question is correctly answered, it is “done” and can offer no further learning moments. Thinking such a question to be boring and unchallenging, some people even yawn at the idea of revising it. Don’t make this error. When choosing questions for revision, choose:
- not only the ones that you answered incorrectly,
- but also those that you answered correctly but
- were initially puzzled by, or
- took a long time to answer, or
- found to be interesting or creative applications of a conceptual point.
This way, you will improve the quantity of questions that you revise.
To improve the quality of your revision, I propose the following two ideas:
1. Get creative with the solutions
2. Get creative with the question
The fundamental assumption that guides these ideas is that even when you have done a question once or twice, it still holds unextracted practice and learning potential. You can tap this latent potential by playing around creatively with the solutions and the question itself.
I will now illustrate both these ideas with a question taken from the GRE Official Guide. Proceed to the demonstration of the first idea only after you have solved (or at least attempted) the question on your own.
The question is this:
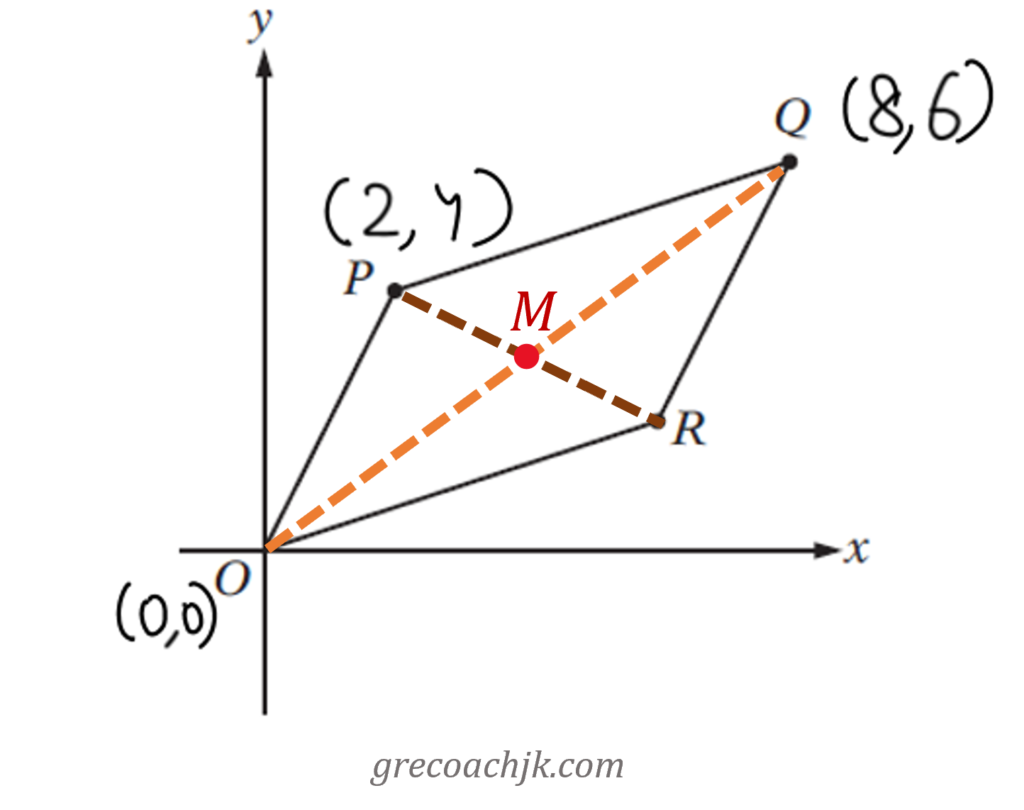
The given figure shows a parallelogram in the x-y coordinate plane and the coordinates of three of its vertices. Find the coordinates of the fourth vertex.
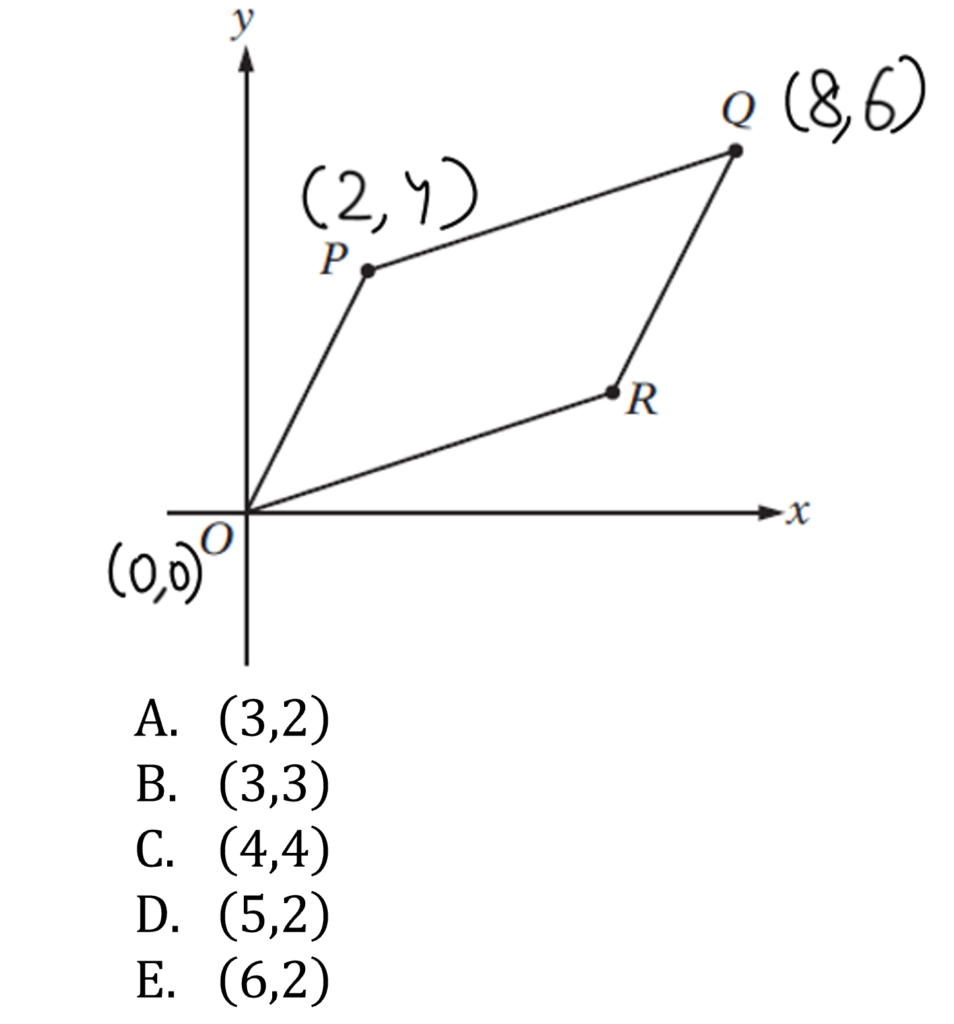
1. Get creative with the Solutions
There are often multiple ways to solve a question.
In your first attempt of a question, how many solutions do you usually think of? If you are like me and most of my students, you’ll probably say ‘one or two.’ Now, if your answer to the question turns out to be correct and, therefore, you never revisit the question, you deprive yourself of the opportunity to search for other possible solutions and of the enjoyment that this playful quest brings; the experience is like solving logical puzzles.
So, the first idea for better revision of quant questions is to revisit a question with the specific goal of thinking up as many alternative solutions for it as you can.
For example, when I implemented this idea for the parallelogram question shared above, I found seven different ways to arrive at the correct answer. I’ll share these in a minute, but would you like to stop here and preempt some of these on your own?
Give it a try. See how many of the seven solutions you can find. (Writing this sentence reminded me of the brainteasers that ask if you can find all the seven differences between two images that superficially look alike. (see example))
Okay, so how many alternative solutions did you find?
The seven that I found are the following. For all these solutions, we’ll assume that the coordinates of point R are (x, y).
Solution 1 – Find slope of a side + Use answer choices
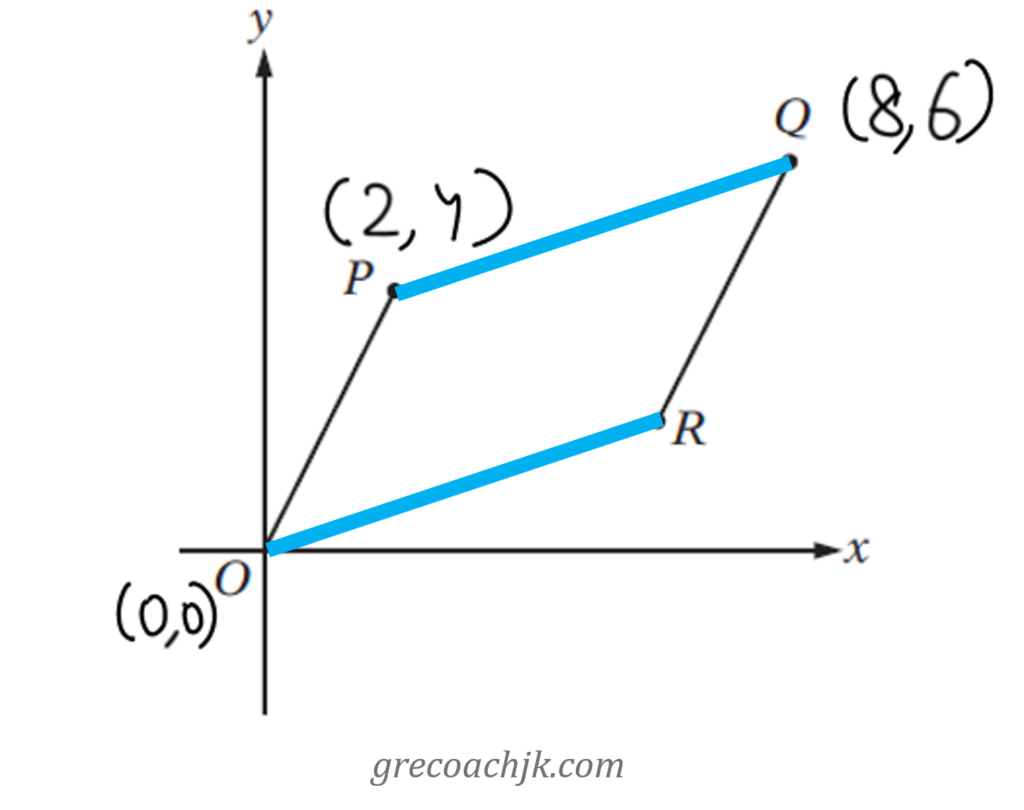
Consider a pair of opposite sides, say PQ and OR.
As OPQR is a parallelogram, the opposite sides OR and PQ are parallel and have the same slope.
Using the coordinates of P and Q, find the slope of PQ. This will also be the slope of OR.
Go through the answer choices one by one. See if the coordinates in an answer choice, when used along with the coordinates of point O in the slope formula, will result in the slope that we now know OR has.
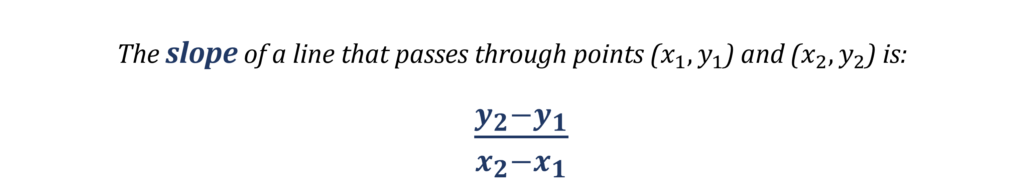
You’ll find that only one option fits this requirement: that’s your answer.
(Note: you could also implement the approach outlined in Solution 1 with the other pair of opposite sides: OP and RQ)
Solution 2 – Find slopes of sides OR and QR
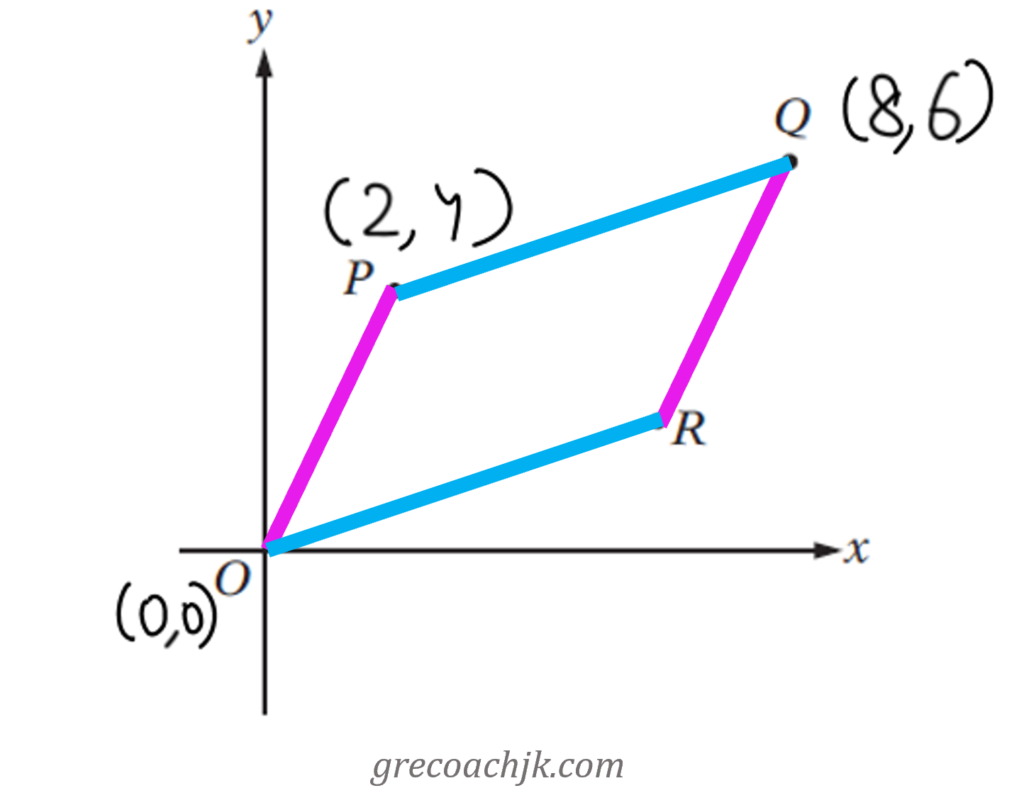
From the fact that (slope of OR) = (slope of PQ), you get this linear equation: x= 3y
And, from the fact that (slope of RQ) = (slope of OP), you get another linear equation: 2x-y=10
Upon solving this pair of equations, you get unique values of x and y.
Solution 3 – Use ‘Opposite sides are parallel and equal’
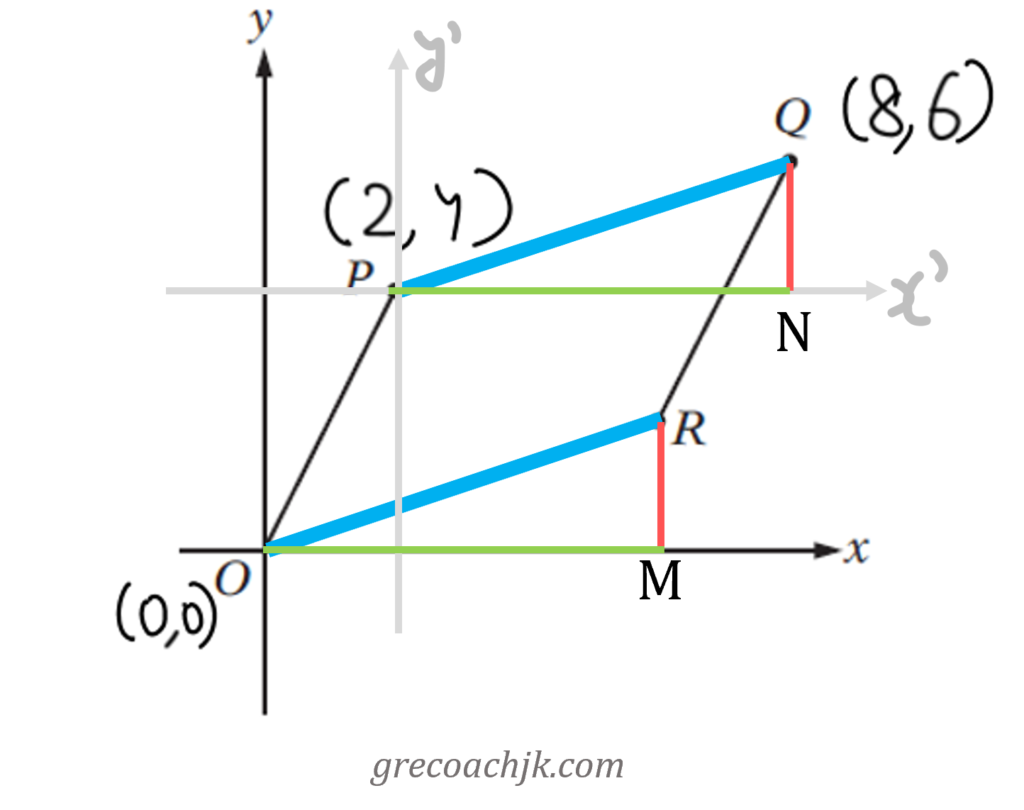
In this approach, we will make use of TWO properties of a parallelogram:
– Opposite sides of a parallelogram are parallel.
– Opposite sides of a parallelogram are equal.
Let’s consider this pair of opposite sides: OR and PQ.
Consider the triangles OMR and PNQ. What is the relationship between them?
They are congruent. So, PN = OM, and NQ = MR
We know the coordinates of P and Q; so, we can find PN and NQ. These lengths will be the same as the lengths of OM and MR, respectively.
Then, using the coordinates of point O, we can determine the coordinates of point R.
The same approach could be applied to the other pair of opposite sides: OP and RQ.
It’s also interesting at this point to compare Solution 1 with Solution 3:
- In Solution 3, the use of two properties enables us to arrive at the exact answer ourselves, without having to rely on the answer choices.
- In contrast, in Solution 1, we had used only one property of a parallelogram and, therefore, had got only one linear equation. A single linear equation in x and y has infinitely many solutions. It was not sufficient to give us unique coordinates of point R. We reasoned that because this was a single answer question, the coordinate-pair of R was going to be one of the five options presented in the question itself. So, we decided to work with the answer choices, seeing if they fit our equation and eliminating those that didn’t. Luck favored us: only one option survived this elimination process; so, we could be sure that this option was the right answer.
Solution 4 – Solve the equations of lines OR and QR

This solution is based on the observation that R is the intersection point of lines OR and RQ.
Line OR passes through the origin and has a slope of 1/3 (the same slope as PQ).
So, equation of line OR is: y=x/3.
Line QR passes through the point Q (8,6) and has a slope of 2 (the same slope as OP).
So, if you start by writing the equation of line QR as y=2x+c, and then put x=8 and y=6, you can find the equation of line QR.
Now that you have two linear equations in two variables, solve them together and get the coordinates of R.
Solution 5 – Use Distance Formula + Use Answer Choices
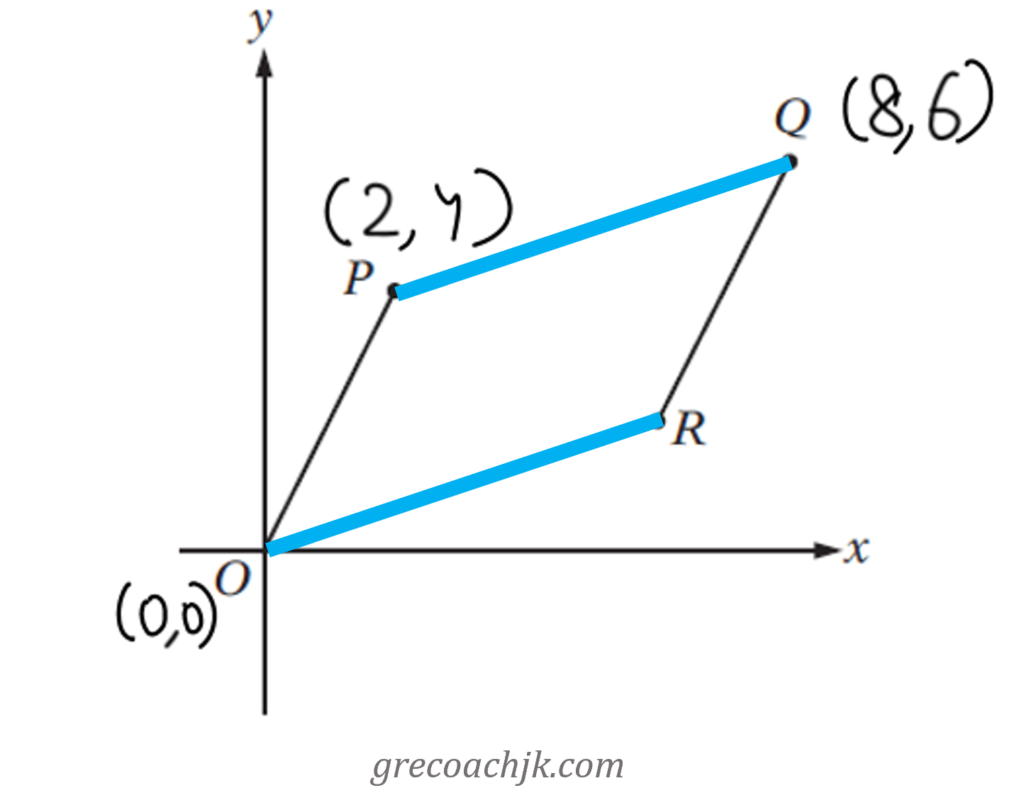
This solution uses the fact that the opposite sides of a parallelogram are equal.
Consider the pair OR and PQ. We know the coordinates of vertices P and Q. Using these in the Distance Formula (which is a simple application of the Pythagoras Theorem), we get:
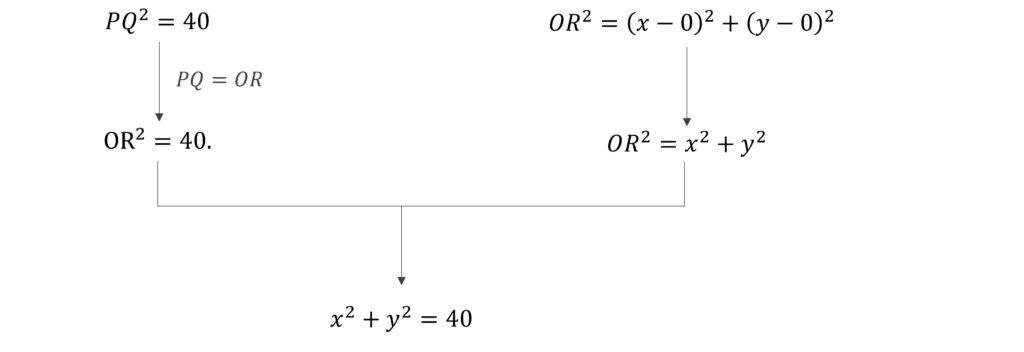
Now, look at the answer choices to see which fits the bill. You’ll find that only one does; so that must be the right answer.
You could also apply the same idea to the other pair of opposite sides: OP and RQ.
Solution 6 – Algebraically solve for ‘Opposite sides are parallel and equal’
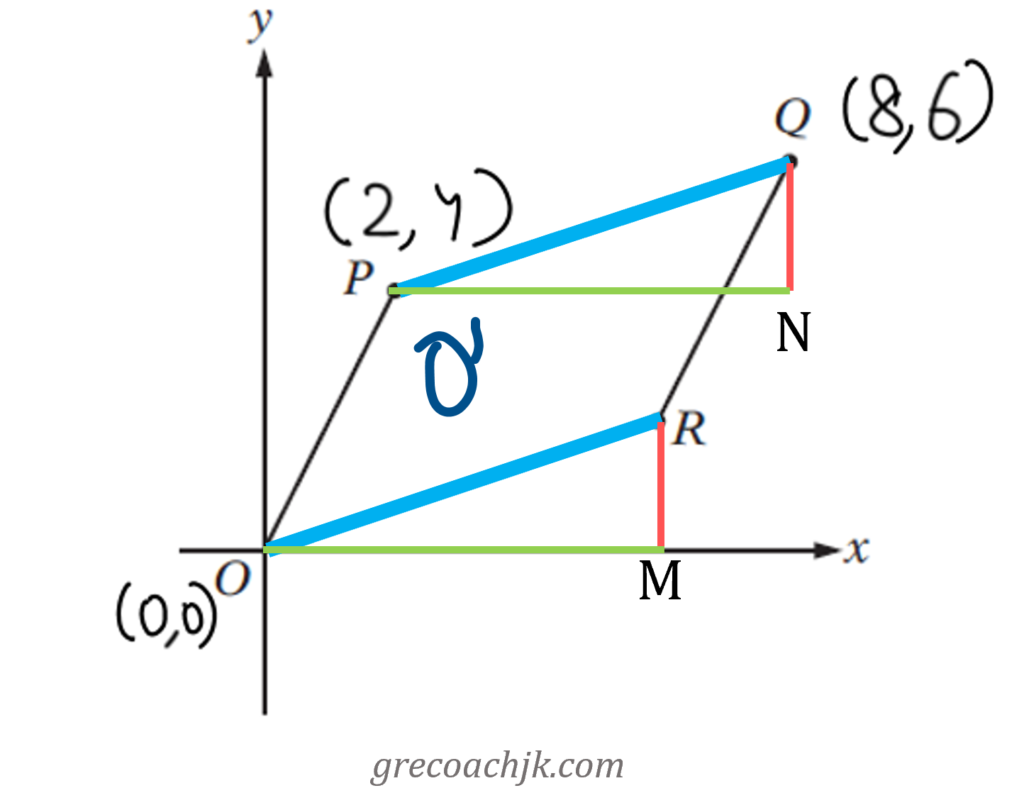
As in solution 5 above, we use the fact that OR=PQ to arrive at the following result:
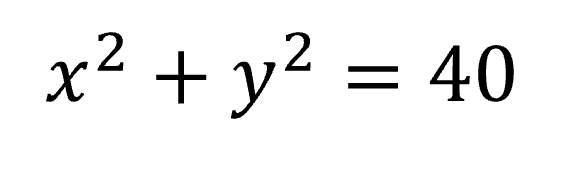
Then, by using the fact that slope of OR equals the slope of PQ, we get the following linear equation in x and y: x=3y
By solving these two equations together, we get two solutions for (x, y): (6, 2) or (-6, -2). Since the given figure unambiguously shows point R to be in the first quadrant, we reject the case of (-6, -2) , and thus arrive at a unique answer.
(If you are wondering about what the two solutions we obtained here (6, 2) and (-6, -2) represent, draw a circle with center at O and radius OR. Points (6,2) and (-6, -2) are the two endpoints of that diameter of this circle which is obtained by extending RO into the third quadrant.)
We could solve the same way with the pair OP and RQ, of course.
It is interesting to compare at this point Solution 6 with Solution 3: both use the same properties, but which do you like more? What takeaway might you draw from this comparison?
Solution 7 – Find mid-point of OQ and PR
The diagonals of a parallelogram bisect one another. This means that if diagonals OQ and PR intersect at point M, then:
OM=MQ, and PM=MR.
Using the mid-point formula on diagonal OQ, we can find the coordinates of M.
Then, by using these coordinates of M when applying the mid-point formula on diagonal PR, you can find the coordinates of R.
End note for Idea 1
So, this was my first idea – think of multiple solutions to the problem at hand. Did you enjoy the exercise? How many of the approaches listed above could you anticipate? Doesn’t the discovery of a different way of looking at a question – a new perspective that was there, shining plainly in the diagram, all the while and that we had somehow still missed – make one go “wow!”? If you came up with still another approach to solve this question and are excited to share it, please message it to me through LinkedIn. I would love to learn the perspectives that I have missed!
2. Get creative with the Questions
The second idea to make your revision more effective is to use an official question as a springboard for further exploration. Ask ‘what if’ questions for the given set-up – what if this condition changed? What if that constraint was not given? What if the point was not here but there? What if I was asked not this but that? – and then try to solve these spin-off questions (I call them Derivative questions).
You may find it interesting that ETS – the organization that conducts the GRE test – also uses this idea to create new test questions. Here is a snapshot taken from the ETS website:

How wonderful would it be to get in the actual test a question that is the same as or quite similar to a derivative question that you created for your practice! You would feel proud of yourself, wouldn’t you?
For the official question discussed above, what Derivative questions might be created? Let’s see.
When you study the set up given in that question, one ‘what-if’ scenario that you could wonder about might be,
“In the original question, they gave me the coordinates of points O, P and Q, and asked me to find the coordinates of point R. What if, instead, I had been given the coordinates of, say, O, P and R; could I have found the coordinates of Q then?”
And so, you get a derivative question such as this one:
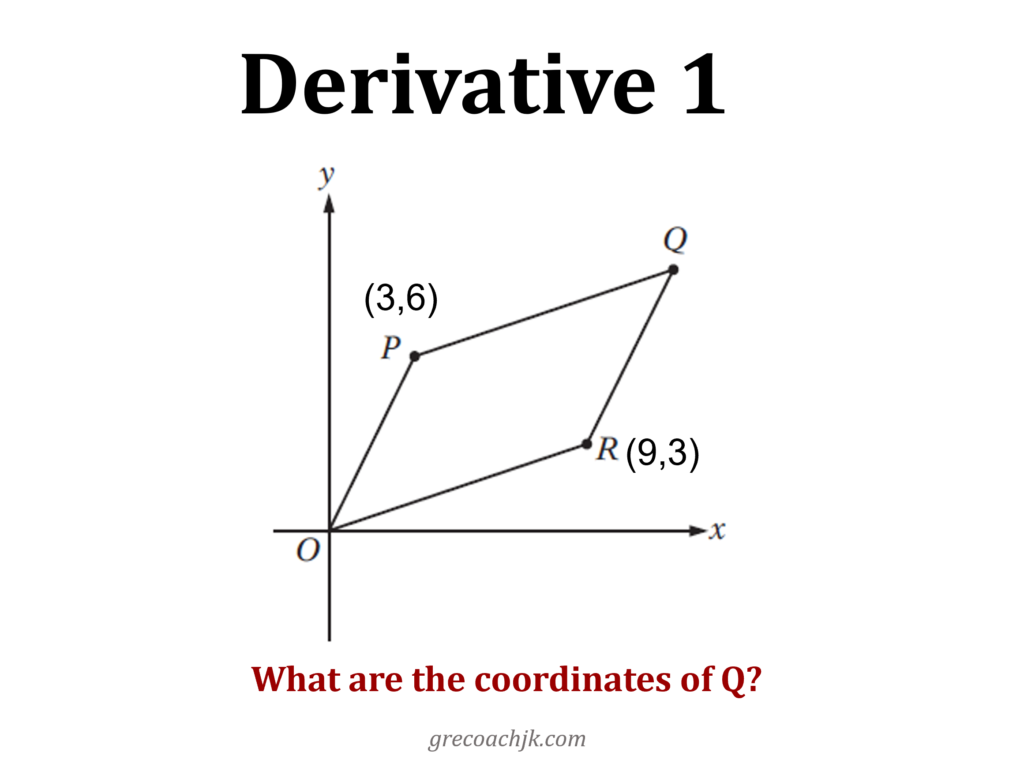
I encourage you to solve this and the subsequent derivative questions. The answers are at the end of this article.
Or, you might think:
“It’s proving to be very convenient for me that point O is at (0,0). Would the question change significantly if the point O was somewhere other than the origin?”
And, so you might think up a scenario such as this:
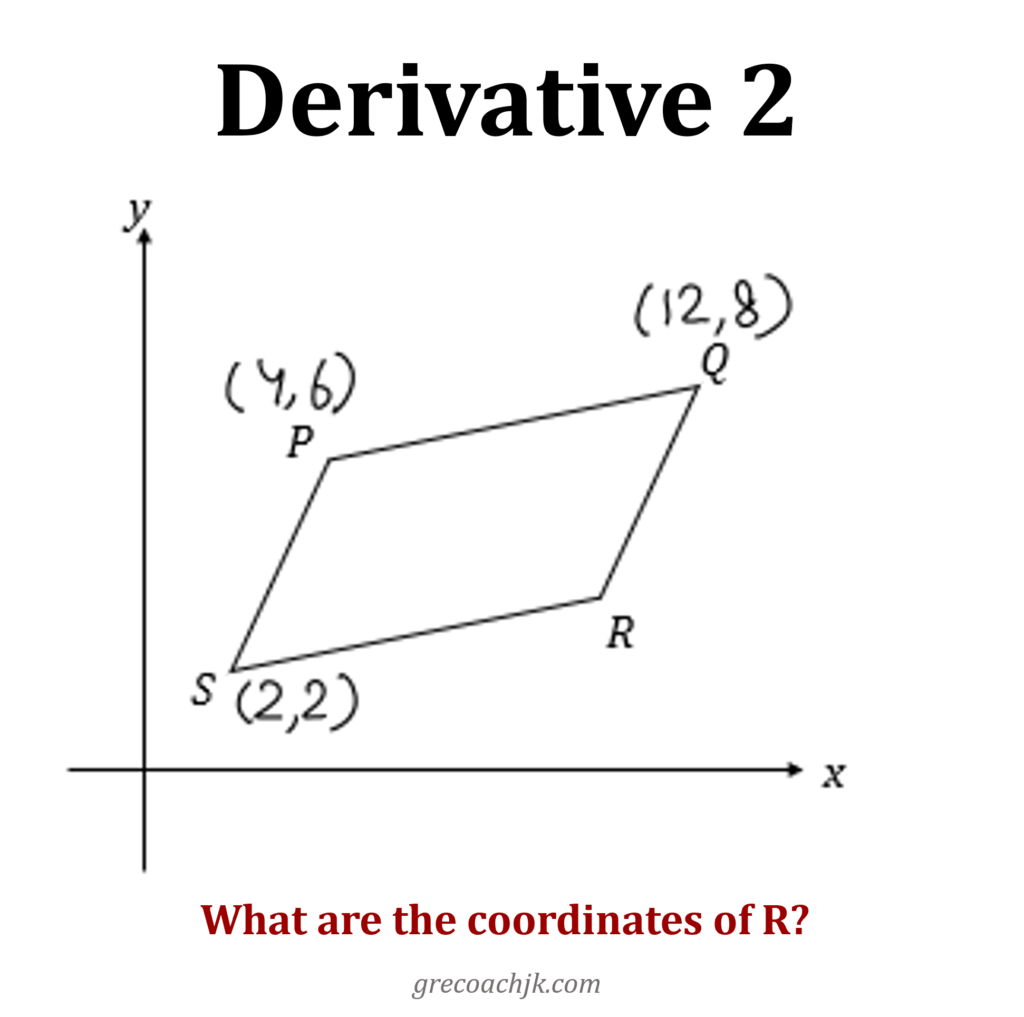
You might even wonder how your solution would change if instead of being a parallelogram, OPQR had been a rectangle instead, and this idea may lead you to a derivative question such as this one:

How would you find the coordinates of R now?
Conclusion
Undoing the Gordian knot had seemed to be a tough, even unsurmountable, challenge till people kept trying to untie it. Once Alexander thought of a creative new solution, the problem suddenly became easy!
This insight applies to GRE quant as well. When a question seems to be difficult or cumbersome, chances are that there are easier, less time consuming, and more elegant solutions to that question that one is not yet able to see. Setting out on a quest to seek these elusive alternative solutions and, therefore, finding them, will probably make one amend their initial unfavorable assessment of the question.
The advantage of creating your own questions is that creation is more active, attentive, and involved than mere consumption. You notice more things about a question, you learn more, and you remember it far better. Also, for your practice, you no longer remain at the mercy of questions-made-by-others. You can create your own practice around the questions and conceptual points that you find to be challenging!
The attitude that I hope to encourage in you is that of confident playfulness around mathematics. Know that the solution provided in a book/course is not the only solution possible. And know that the version of the question provided in the book/course is not the only version possible. You can create your own solutions and your own versions of the question and, therefore, create a deliberate practice exercise that is fully customized to your needs and weaknesses!
I’ll give the last word to Richard Feynman, a brilliant theoretical physicist and a winner of the Nobel Prize in Physics:
“To use mathematics successfully one must have a certain attitude of mind – to know that there are many ways to look at any problem and at any subject. . . We must leave freedom for the mind to wander about in trying to solve problems. . . You need an answer for a certain problem: the question is how to get it. The successful user of mathematics is practically an inventor of new ways of obtaining answers in given situations. Even if the ways are well known, it is usually much easier for him to invent his own way – a new way or an old way – than it is to try to find an answer by looking it up. The question he asks himself is not, “What is the right way to do this problem?” It is only necessary that he get the right answer.
What is the best method to obtain the solution to a problem? The answer is, any way that works. [A successful user of mathematics shows] flexibility of mind – the various possible ways of writing down a problem, the possible ways of thinking about it, and the possible ways of getting at the problem.”
Richard Feynman, Don’t You Have Time to Think, Page 447.
Answers to the derivative questions:
Derivative 1: Coordinates of point Q are (12, 9)
Derivative 2: Coordinates of point R are (10, 4)
Derivative 3: Coordinates of point R are (8, 6)
Note: This article is also published on LinkedIn.